Ctrl+K

Three-dimensional limit analysis problem using Semi-Definite Programming

Three-dimensional limit analysis problem using Semi-Definite Programming#

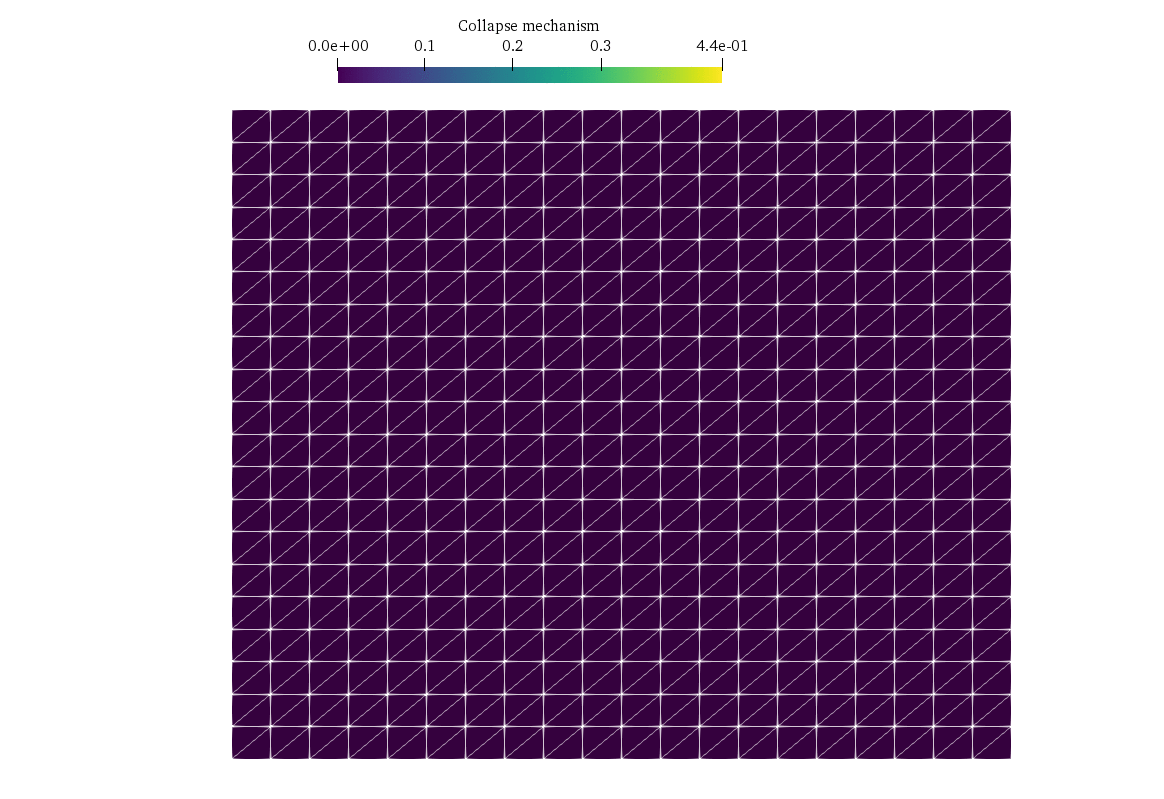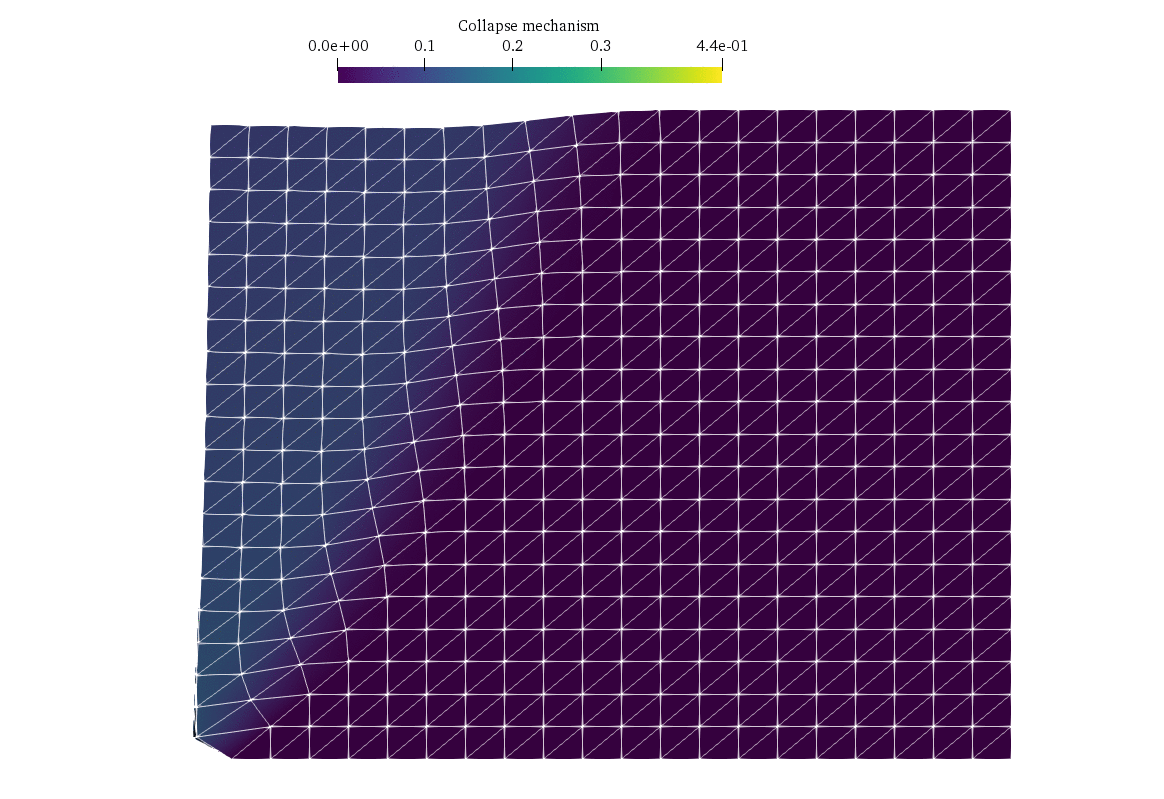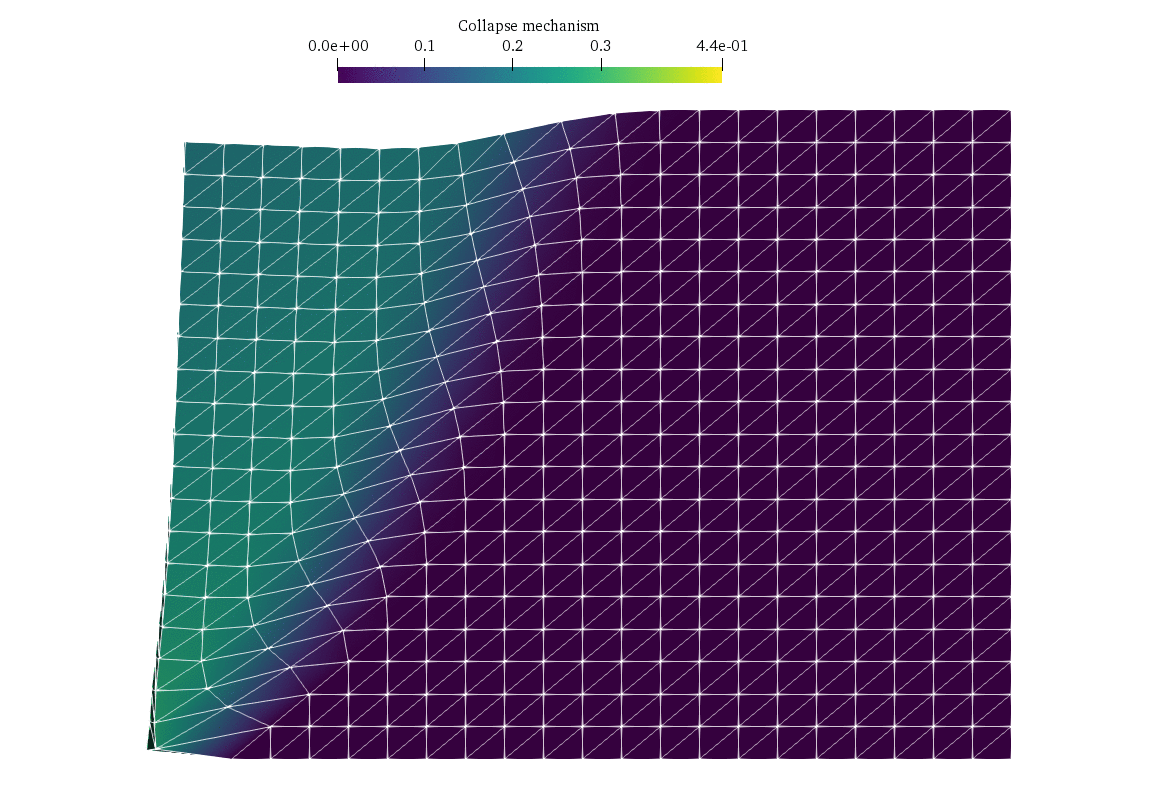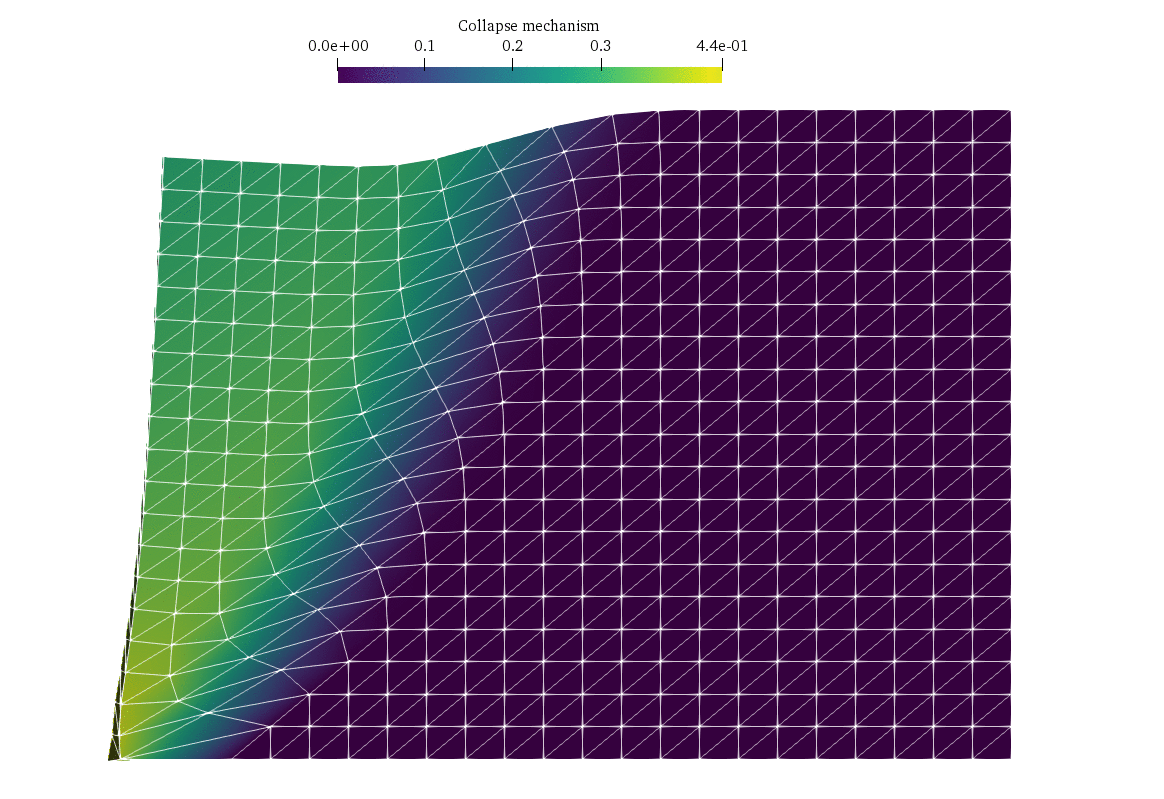
In this demo, we consider a classical limit analysis problem, namely a slope stability problem for a cohesive-frictional material described by a Mohr-Coulomb criterion. The geometry being three-dimensional in this example, the corresponding problem will be a Semi-Definite Programming (SDP) problem. We show how to formulate such constraints using the dolfinx_optim package.

In the following, we will denote by \(\mathbb{S}_n\) the set of symmetric \(n\times n\) matrices.

Problem formulation#

We consider a soil domain \(\Omega = [0;L]\times [0;W] \times [0;H]\) with homogeneous Dirichlet boundary conditions \(\boldsymbol{u}=0\) on the right \(x=L\) and bottom \(z=0\). The remaining boundaries have homogeneous Neumann boundary conditions. The loading consists of a gravitational body force \(\boldsymbol{f}=(0,0,-\gamma)\) with \(\gamma\) being the soil self-weight. The soil obeys a Mohr-Coulomb criterion of cohesion \(c\) and internal friction angle \(\phi\), i.e. the stress state \(\boldsymbol{\sigma}\in \mathbb{S}_3\) must satisfy \(\boldsymbol{\sigma}\in G\) where:

(1)#\[\begin{equation} G=\left\{\boldsymbol{\sigma}\in \mathbb{S}_3 \text{ s.t. } \sigma_M - a\sigma_m \leq \dfrac{2c\cos\phi}{1+\sin\phi}\right\} \end{equation}\]

where \(a=\dfrac{1-\sin\phi}{1+\sin\phi}\), \(\sigma_M = \max_{I} \{\sigma_I\}\) and \(\sigma_m = \min_I \{\sigma_I\}\) with \(\sigma_I\) being the eigenvalues of \(\boldsymbol{\sigma}\).

The limit analysis problem amounts to finding the slope stability factor given by \(SF=\lambda^+\dfrac{\gamma H}{c}\) where \(\lambda^+\) is obtained from solving:

(2)#\[\begin{equation} \begin{array}{rl} \displaystyle{\lambda^+ = \inf_{\boldsymbol{u}}} & \displaystyle{\int_\Omega \pi(\nabla^s \boldsymbol{u}) \,\text{d}\Omega}\\ \text{s.t.} & \displaystyle{\int_{\Omega} \boldsymbol{f}\cdot\boldsymbol{u} \,\text{d}\Omega = 1} \end{array} \end{equation}\]

in which \(\nabla^s \boldsymbol{u} = \frac{1}{2}(\nabla \boldsymbol{u} + \nabla \boldsymbol{u}^T)\) is the symmetric gradient and \(\pi\) is the support function of the convex set \(G\):

\[\begin{align*} \pi(\boldsymbol{d}) &= \sup_{\boldsymbol{\sigma}\in G} \{\boldsymbol{\sigma}:\boldsymbol{d}\}\\ &= \begin{cases} c \cot\phi \operatorname{tr}(\boldsymbol{d}) & \text{if } \displaystyle{\operatorname{tr}(\boldsymbol{d}) \geq \sin\phi\left(\sum_I |d_I|\right)} \\ +\infty & \text{otherwise} \end{cases} \end{align*}\]

Conic reformulation#

Following [Martin and Makrodimopoulos, 2008], the above support function can be expressed equivalently in a conic-representable fashion using two auxiliary SDP variables \(\boldsymbol{Y}_1,\boldsymbol{Y}_2\) as follows:

(3)#\[\begin{equation} \begin{array}{rl} \displaystyle{\pi(\boldsymbol{d}) = \inf_{\boldsymbol{Y}_1,\boldsymbol{Y}_2\in \mathbb{S}_3}} & \dfrac{2c\cos\phi}{1+\sin\phi}\operatorname{tr}(\boldsymbol{Y}_1)\\ \text{s.t.} & \boldsymbol{d} = \boldsymbol{Y}_1 - \boldsymbol{Y}_2\\ & a\operatorname{tr}(\boldsymbol{Y}_1)=\operatorname{tr}(\boldsymbol{Y}_2)\\ & \boldsymbol{Y}_1 \succeq 0, \boldsymbol{Y}_2\succeq 0 \end{array} \end{equation}\]

Implementation#

We first important relevant packages and define the box mesh.

from mpi4py import MPI
import numpy as np
import ufl
from dolfinx import mesh, fem, io
from dolfinx_optim.mosek_io import MosekProblem
from dolfinx_optim.convex_function import ConvexTerm
from dolfinx_optim.cones import SDP
from dolfinx_optim.utils import to_vect

L, W, H = (1.2, 2.0, 1.0)
Nx, Ny, Nz = (20, 1, 20)
domain = mesh.create_box(MPI.COMM_WORLD, [(0, 0, 0), (L, W, H)], [Nx, Ny, Nz])

Note that we used on purpose only 1 element in the \(y\)-direction with quite a large width in order to reproduce a 2D plane-strain situation for which we have a good approximation of the exact solution and limit the computation time of this demo.

We then define the conic representation of the Mohr-Coulomb support function:

c = fem.Constant(domain, 1.0)
phi = fem.Constant(domain, np.pi / 6.0)


class MohrCoulomb(ConvexTerm):
    """SDP implementation of Mohr-Coulomb criterion."""

    def conic_repr(self, X):
        Y1 = self.add_var((3,3), cone=SDP(3))
        Y2 = self.add_var((3,3), cone=SDP(3))
        a = (1 - ufl.sin(phi)) / (1 + ufl.sin(phi))
        self.add_eq_constraint(X - to_vect(Y1) + to_vect(Y2))
        self.add_eq_constraint(ufl.tr(Y2) - a * ufl.tr(Y1))
        self.add_linear_term(2 * c * ufl.cos(phi) / (1 + ufl.sin(phi)) * ufl.tr(Y1))

In the above, symmetric \(n\times n\) matrix variables are created. The SDP constraint is enforced through the cone SDP(3). Note that equality constraints expect scalar or vectors so that we use the to_vect utility function to reshape the matrix variables to a vector form.

We can now set up the loading, function spaces and boundary conditions:

gamma = 10.0
f = fem.Constant(domain,(0, 0, -gamma))

def border(x):
    return np.isclose(x[0], L) | np.isclose(x[2], 0)


gdim = 3
V = fem.functionspace(domain, ("CG", 2, (gdim,)))
bc_dofs = fem.locate_dofs_geometrical(V, border)
bcs = [fem.dirichletbc(np.zeros((gdim,)), bc_dofs, V)]

We now initiate the MosekProblem object and first add the linear equality constraint:

prob = MosekProblem(domain, "3D limit analysis")
u = prob.add_var(V, bc=bcs, name="Collapse mechanism")


prob.add_eq_constraint(ufl.dot(f,u)*ufl.dx, b=1.0)

We now add the convex term corresponding to the support function.

crit = MohrCoulomb(ufl.sym(ufl.grad(u)), 2)
prob.add_convex_term(crit)

The problem can then be solved and results are exported to Paraview.

pobj, dobj = prob.optimize()

with io.VTKFile(MPI.COMM_WORLD, "results.pvd", "w") as vtk:
    vtk.write_function(u)
Hide code cell output 
Problem

  Name                   : 3D limit analysis

  Objective sense        : minimize        

  Type                   : CONIC (conic optimization problem)

  Constraints            : 96730           

  Affine conic cons.     : 0               

  Disjunctive cons.      : 0               

  Cones                  : 0               

  Scalar variables       : 15130           

  Matrix variables       : 19200 (scalarized: 115200)

  Integer variables      : 0               



Optimizer started.

GP based matrix reordering started.

GP based matrix reordering terminated.

Optimizer  - threads                : 14              

Optimizer  - solved problem         : the primal      

Optimizer  - Constraints            : 96730           

Optimizer  - Cones                  : 1               

Optimizer  - Scalar variables       : 15130             conic                  : 15130           

Optimizer  - Semi-definite variables: 19200             scalarized             : 115200          

Factor     - setup time             : 2.80            

Factor     - dense det. time        : 1.15              GP order time          : 0.21            

Factor     - nonzeros before factor : 3.89e+06          after factor           : 6.91e+06        

Factor     - dense dim.             : 11786             flops                  : 5.47e+11        

Factor     - GP saved nzs           : 5.44e+05          GP saved flops         : 2.37e+09        

ITE PFEAS    DFEAS    GFEAS    PRSTATUS   POBJ              DOBJ              MU       TIME  

0   6.4e+01  1.0e+00  9.3e+00  0.00e+00   8.313843876e+00   0.000000000e+00   1.0e+00  2.91  

1   6.0e+01  9.4e-01  4.2e+01  -1.96e+01  2.057973683e+01   2.220911241e+01   9.4e-01  5.91  

2   5.4e+01  8.5e-01  6.3e+01  -3.74e+01  1.541073344e+00   6.470667017e+01   8.5e-01  8.67  

3   4.3e+01  6.8e-01  6.1e+01  -1.94e+00  1.953587175e+00   9.416024834e+01   6.8e-01  11.41 

4   3.0e+01  4.7e-01  5.3e+01  -1.69e+00  2.877919262e+00   1.476198772e+02   4.7e-01  14.15 

5   1.0e+01  1.6e-01  2.4e+01  -1.15e+00  9.257383903e+00   2.735340275e+02   1.6e-01  17.16 

6   2.3e+00  3.6e-02  2.7e+00  2.91e-01   1.778475369e+01   7.996443998e+01   3.6e-02  20.47 

7   4.0e-01  6.2e-03  4.7e-02  1.26e+00   3.875455863e+00   4.510374853e+00   6.2e-03  23.84 

8   1.9e-01  3.0e-03  1.3e-02  4.28e+00   1.289498450e+00   1.509526752e+00   3.0e-03  26.75 

9   9.9e-02  1.5e-03  4.1e-03  2.09e+00   9.199815082e-01   9.991602610e-01   1.5e-03  29.66 

10  5.6e-02  8.7e-04  1.5e-03  1.53e+00   8.107590068e-01   8.460483001e-01   8.7e-04  32.56 

11  1.0e-02  1.6e-04  7.5e-05  1.31e+00   7.169651108e-01   7.194055361e-01   1.6e-04  35.80 

12  1.9e-03  3.0e-05  2.7e-06  1.06e+00   6.994801453e-01   6.995547014e-01   3.0e-05  39.31 

13  4.0e-04  6.3e-06  1.3e-07  1.01e+00   6.958774407e-01   6.958786193e-01   6.3e-06  42.89 

14  1.7e-04  2.7e-06  3.0e-08  1.00e+00   6.953302559e-01   6.953302373e-01   2.7e-06  45.92 

15  2.9e-05  4.5e-07  6.2e-10  1.00e+00   6.949877854e-01   6.949875713e-01   4.5e-07  49.40 

16  1.6e-05  2.5e-07  2.4e-10  9.97e-01   6.949594176e-01   6.949592945e-01   2.5e-07  52.65 

17  8.4e-07  3.7e-08  4.3e-12  9.96e-01   6.949278248e-01   6.949278054e-01   3.7e-08  56.20 

Optimizer terminated. Time: 56.29   





Interior-point solution summary

  Problem status  : PRIMAL_AND_DUAL_FEASIBLE

  Solution status : OPTIMAL

  Primal.  obj: 6.9492782476e-01    nrm: 1e+01    Viol.  con: 3e-06    var: 0e+00    barvar: 0e+00  

  Dual.    obj: 6.9492780542e-01    nrm: 8e-01    Viol.  con: 0e+00    var: 8e-11    barvar: 2e-09

We can then check the solution compared with the exact solution provided by [Chen, 2013].

print("2D factor [Chen] (for phi=30°):", 6.69)
print("Computed factor:", pobj*float(gamma*H/c))

2D factor [Chen] (for phi=30°): 6.69
Computed factor: 6.949278247567571

References#

[Che13]

Wai-Fah Chen. Limit analysis and soil plasticity. Elsevier, 2013.

[MM08]

Christopher M Martin and Athanasios Makrodimopoulos. Finite-element limit analysis of mohr–coulomb materials in 3d using semidefinite programming. Journal of engineering mechanics, 134(4):339–347, 2008.

Contents