Finite-strain \(\boldsymbol{F}^\text{e}\boldsymbol{F}^\text{p}\) plasticity#
\(\newcommand{\bF}{\boldsymbol{F}}\newcommand{\bFe}{\boldsymbol{F}^\text{e}}\newcommand{\bFp}{\boldsymbol{F}^\text{p}}\)
In this example, we show how to use a JAX implementation of finite-strain plasticity using the \(\bFe\bFp\) formalism. The material behavior is described in the jaxmat documentation.
The setup of the FEniCSx variational problem is quite similar to the MFront Finite-strain elastoplasticity within the logarithmic strain framework demo.
This demo runs in parallel. By default, JAX will allocate the full GPU memory for each process, which will fail when running with more than 1 MPI processor. Thus we first deallocate automatic GPU memory preallocation. The relevant packages are then imported.
import os
from mpi4py import MPI
# Avoid JAX preallocating all GPU memory
os.environ["XLA_PYTHON_CLIENT_PREALLOCATE"] = "false"
# --- Import JAX AFTER setting env vars ---
import jax
jax.config.update("jax_platform_name", "gpu")
import numpy as np
from pathlib import Path
import gmsh
import ufl
from dolfinx import fem, io
from dolfinx.common import timing
from dolfinx_materials.quadrature_map import QuadratureMap
from dolfinx_materials.solvers import NonlinearMaterialProblem
from dolfinx_materials.utils import nonsymmetric_tensor_to_vector
import jaxmat.materials as jm
from dolfinx_materials.jaxmat import JAXMaterial
comm = MPI.COMM_WORLD
rank = comm.rank
dim = 3
L = 10.0 # rod half-length
W = 2.0 # rod diameter
R = 20.0 # notch radius
d = 0.2 # cross-section reduction
coarse_size = 0.5
fine_size = 0.2
W1120 22:20:38.889384 69573 cuda_executor.cc:1802] GPU interconnect information not available: INTERNAL: NVML library doesn't have required functions.
W1120 22:20:38.891780 69413 cuda_executor.cc:1802] GPU interconnect information not available: INTERNAL: NVML library doesn't have required functions.
The mesh consists of a quarter of cylindrical rod with a slightly reduced cross-section at its center to induce necking. The geometry is defined with gmsh API and the Open-Cascade kernel.
Horizontal traction with free transverse displacement is imposed at the rod extremities, symmetry boundary conditions are enforced on other plane surfaces.
fdim = dim - 1
domain.topology.create_connectivity(fdim, dim)
order = 2
V = fem.functionspace(domain, ("P", order, (dim,)))
deg_quad = 2 * (order - 1)
V_x, _ = V.sub(0).collapse()
V_y, _ = V.sub(1).collapse()
V_z, _ = V.sub(2).collapse()
bottom_x_dofs = fem.locate_dofs_topological((V.sub(0), V_x), fdim, facets.find(1))
top_x_dofs = fem.locate_dofs_topological((V.sub(0), V_x), fdim, facets.find(4))
side_y_dofs = fem.locate_dofs_topological((V.sub(1), V_y), fdim, facets.find(2))
side_z_dofs = fem.locate_dofs_topological((V.sub(2), V_z), fdim, facets.find(3))
u0_x = fem.Function(V_x)
u0_y = fem.Function(V_y)
u0_z = fem.Function(V_z)
uD_x = fem.Function(V_x)
bcs = [
fem.dirichletbc(u0_y, bottom_x_dofs, V.sub(0)),
fem.dirichletbc(u0_y, side_y_dofs, V.sub(1)),
fem.dirichletbc(u0_z, side_z_dofs, V.sub(2)),
fem.dirichletbc(uD_x, top_x_dofs, V.sub(0)),
]
As in the MFront hyperelastic demo, the nonlinear residual based on PK1 stress is used. The jaxmat FeFpJ2Plasticity behavior is defined based on an elastic material and a Voce isotropic hardening.
Id = ufl.Identity(dim)
def F(u):
return nonsymmetric_tensor_to_vector(Id + ufl.grad(u))
def dF(u, v):
return ufl.derivative(F(u), u, v)
du = ufl.TrialFunction(V)
v = ufl.TestFunction(V)
u = fem.Function(V, name="Displacement")
E = 70e3
nu = 0.3
sig0 = 500.0
b = 1000
sigu = 750.0
elasticity = jm.LinearElasticIsotropic(E=E, nu=nu)
hardening = jm.VoceHardening(sig0=sig0, sigu=sigu, b=b)
behavior = jm.FeFpJ2Plasticity(elasticity=elasticity, yield_stress=hardening)
material = JAXMaterial(behavior)
qmap = QuadratureMap(domain, deg_quad, material)
qmap.register_gradient("F", F(u))
P = qmap.fluxes["PK1"]
Res = ufl.dot(P, dF(u, v)) * qmap.dx
Jac = qmap.derivative(Res, u, du)
This material model relies on an elastic left Cauchy-Green internal state variable \(\overline{\boldsymbol{b}}^\text{e}\) describing the intermediate elastic configuration. The latter is automatically initialized with the identity tensor to specify a natural unstressed elastic configuration. We use a first call to the material update function to enforce compilation of the JAX behavior.
qmap.update()
Resolution#
We now define a custom nonlinear problem and pass the corresponding SNES options. We use a GMRES Krylov solver and a Geometric Algebraic MultiGrid preconditioner.
petsc_options = {
"snes_type": "newtonls",
"snes_linesearch_type": "none",
"snes_atol": 1e-8,
"snes_rtol": 1e-8,
"ksp_type": "gmres",
"ksp_rtol": 1e-8,
"pc_type": "gamg",
}
problem = NonlinearMaterialProblem(
qmap,
Res,
u,
bcs=bcs,
J=Jac,
petsc_options_prefix="elastoplasticity",
petsc_options=petsc_options,
)
# -
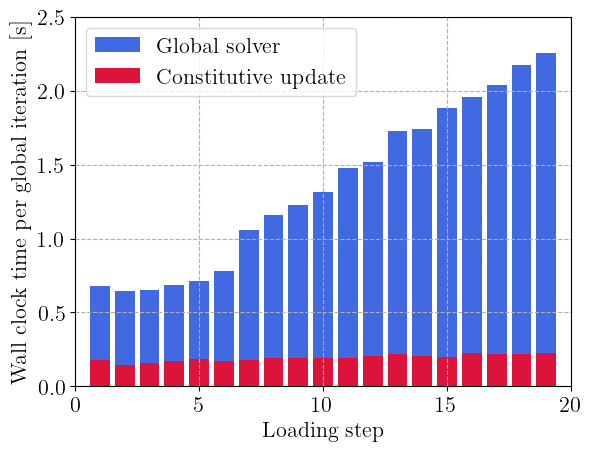
We loop over an imposed increasing horizontal strain and solve the nonlinear problem. We output the displacement and equivalent plastic strain variables. Finally, we measure the time spent by each rank on the constitutive update and the SNES solver and print the average values on rank 0.
results_folder = Path("results")
results_folder.mkdir(exist_ok=True, parents=True)
filename = results_folder / "finite_strain_plasticity"
V0 = fem.functionspace(domain, ("DG", 0))
p = fem.Function(V0, name="p")
vtx = io.VTXWriter(domain.comm, filename.with_suffix(".bp"), [u, p])
N = 20
Exx = np.linspace(0, 30e-3, N + 1)
average_stats = np.zeros((N, 3))
for i, exx in enumerate(Exx[1:]):
uD_x.x.petsc_vec.set(exx * L)
problem.solve()
converged = problem.solver.getConvergedReason()
num_iter = problem.solver.getIterationNumber()
assert converged > 0, f"Solver did not converge, got {converged}."
constitutive_update_time = timing("SNES: constitutive update")[1].total_seconds()
snes_time = timing("SNES: solve")[1].total_seconds()
all_stats = None
if rank == 0:
all_stats = np.zeros((comm.size, 3))
comm.Gather(
np.array([constitutive_update_time, snes_time, num_iter]), all_stats, root=0
)
if rank == 0:
average_stats[i, :] = np.mean(all_stats, axis=0)
print(
f"Increment {i} converged after {num_iter} iterations with converged reason {converged}.\n"
)
print(f"Dolfinx SNES time = {average_stats[i, 1]:.3f}")
print(f"Pure solver time = {average_stats[i, 1]-average_stats[i, 0]:.3f}")
print(f"Constitutive update time = {average_stats[i, 0]:.3f}\n")
qmap.project_on("p", ("DG", 0), fun=p)
vtx.write(i + 1)
np.savetxt(
filename.with_suffix(".csv"),
average_stats,
delimiter=",",
header="Constitutive update time, SNES solve, num iterations",
)
vtx.close()
import matplotlib.pyplot as plt
num_iter = average_stats[:, 2]
constitutive_time = np.diff(average_stats[:, 0], prepend=average_stats[0, 0]) / num_iter
solver_time = np.diff(average_stats[:, 1], prepend=average_stats[0, 1]) / num_iter
plt.bar(
np.arange(N),
solver_time,
color="royalblue",
label="Global solver",
)
plt.bar(np.arange(N), constitutive_time, color="crimson", label="Constitutive update")
plt.xlabel("Loading step")
plt.ylabel("Wall clock time per global iteration [s]")
plt.xlim(0, N)
plt.legend()
plt.show()