JAX implementation of material behaviors

JAX implementation of material behaviors#

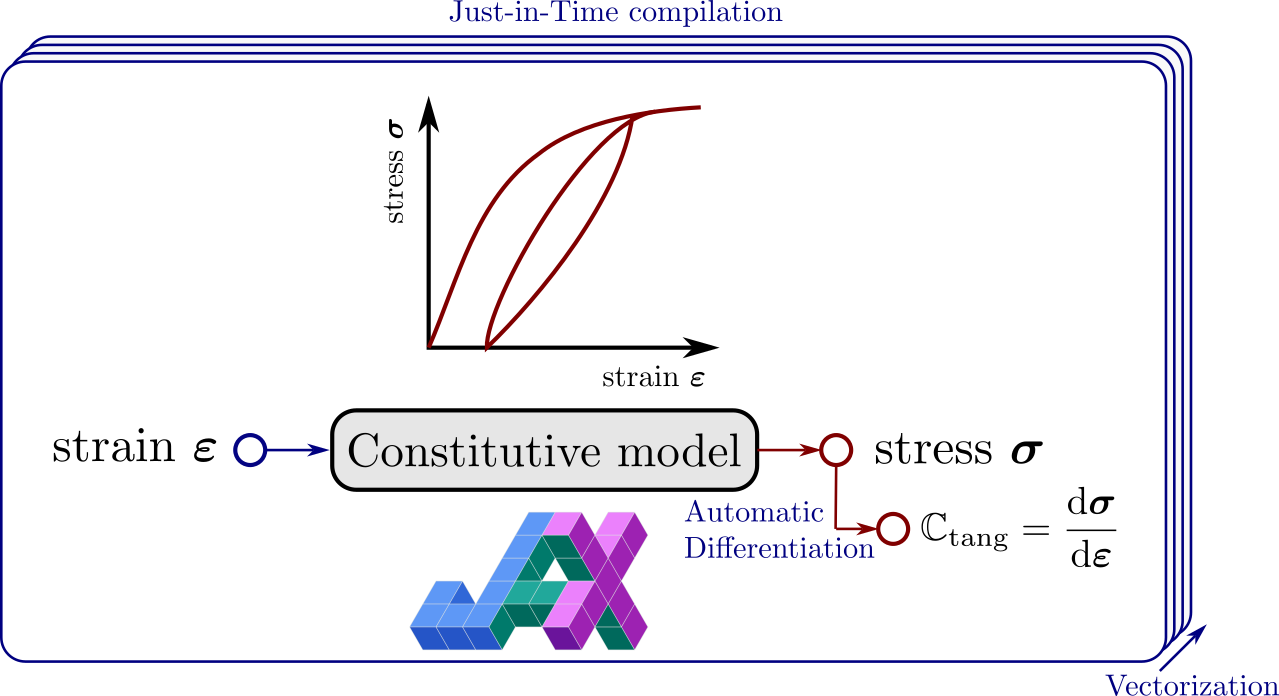
_images/jax_framework.png

The constitutive update of complex behaviors requires:

  • looping over all quadrature points

  • solving evolution equations for internal state variables

  • computing the resulting stress

  • computing the corresponding consistent tangent operator

A pure Python implementation generally prove extremely inefficient due to the loop over all quadrature points. To solve this issue, we will rely on the jaxmat library which implements constitutive models in JAX.

JAX is a Python library for accelerated (GPU) array computation and program transformation, designed for high-performance numerical computing and large-scale machine learning [Bradbury et al., 2018]. Its key features of interest here involve:

All such features prove extremely valuable when implementing optimized constitutive behavior models.

See also

JAX-based behaviors in FEniCSx have been first proposed in and in [Latyshev et al., 2025].

jaxmat#

jaxmat is a JAX-based material modeling library for implementing material constitutive models in a way that integrates seamlessly with modern machine learning frameworks and existing finite element software.

We give below a very brief overview of the features used within dolfinx_materials. For more details on jaxmat implementations of material models or their identification, we refer to the jaxmat documentation.

Composition and hybrid ML-components#

jaxmat behaviors are defined in a modular fashion by composing different sub-entities which are equinox.Modules. Formally, this means that constitutive models are treated exactly as ML models such as neural networks. As a result, jaxmat can also be used to train ML-based constitutive models, which can then be used within FEniCSx using dolfinx_materials.

Batching#

jaxmat tackles the definition of the material constitutive model and its solving methods at the quadrature point level. By leveraging jax.vmap we obtain a batched version of the constitutive update which allows to compute in parallel the current stress of many independent material points.

The JAXMaterial class inherits from the general Material class and provides an interface between dolfinx_materials and any jaxmat behavior.

Each jaxmat behavior implements a constitutive_update method taking as arguments, the current strain eps, the previous state state and the time step dt and returns the current stress sig and the new state new_state as follows:

sig, new_state = material.constitutive_update(eps, state, dt)

where material is a PyTree which implicitly stores learned/calibrated material parameters.

JIT and automatic vectorization#

As stated before, a Python loop over all quadrature points is avoided by leveraging jax.vmap which automatically transforms a function into an efficient vectorized form using jax.vmap.

Moreover, the resulting function is also jitted using jax.jit for efficient compilation and execution by the XLA compiler. Note that jitting induces an extra compilation cost at the first execution of the constitutive integration.

Automatic differentiation#

Finally, we also leverage Automatic Differentiation (AD) to differentiate the constitutive_update method with respect to its first argument, namely the imposed strain \(\boldsymbol{\varepsilon}\) using forward AD with jax.jacfwd.

References#

[BFH+18]

James Bradbury, Roy Frostig, Peter Hawkins, Matthew James Johnson, Chris Leary, Dougal Maclaurin, George Necula, Adam Paszke, Jake VanderPlas, Skye Wanderman-Milne, and Qiao Zhang. JAX: composable transformations of Python+NumPy programs. 2018. URL: google/jax.

[LBMH25]

Andrey Latyshev, Jérémy Bleyer, Corrado Maurini, and Jack Hale. Expressing general constitutive models in fenicsx using external operators and algorithmic automatic differentiation. Journal of Theoretical, Computational and Applied Mechanics, 2025.

Contents