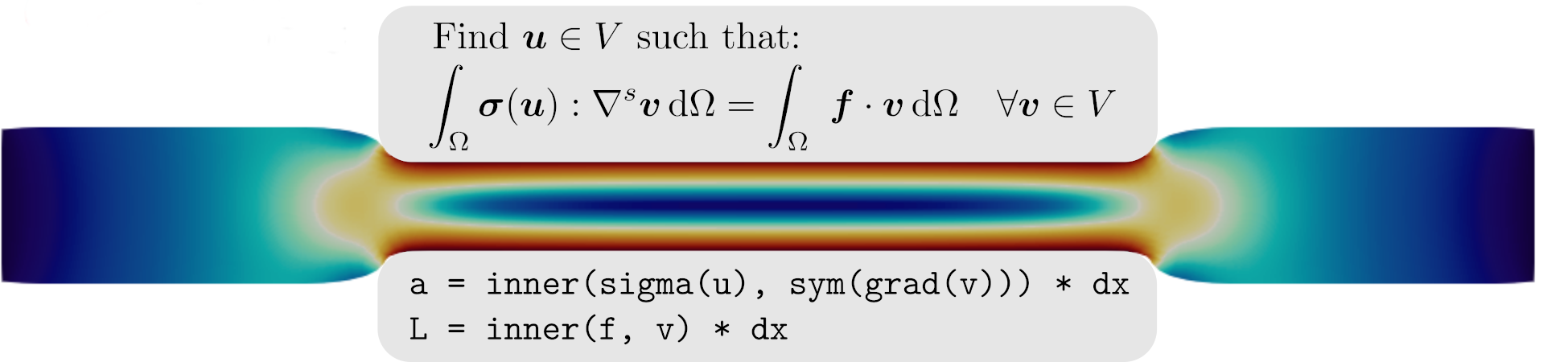Hyperelasticity#
Objectives
In this tour, we will build upon the previous one on linear elasticity to formulate a non-linear problem arising from finite-strain elasticity. The symbolic differentiation capabilities of UFL prove to be very useful in such examples. \(\newcommand{\bsig}{\boldsymbol{\sigma}} \newcommand{\beps}{\boldsymbol{\varepsilon}} \newcommand{\bu}{\boldsymbol{u}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bT}{\boldsymbol{T}} \newcommand{\bC}{\boldsymbol{C}} \newcommand{\bF}{\boldsymbol{F}} \newcommand{\bI}{\boldsymbol{I}} \newcommand{\bP}{\boldsymbol{P}} \newcommand{\dOm}{\,\text{d}\Omega} \newcommand{\dS}{\,\text{d}S} \newcommand{\T}{{}^\text{T}} \newcommand{\tr}{\operatorname{tr}} \newcommand{\Neumann}{{\partial \Omega_\text{N}}} \newcommand{\Dirichlet}{{\partial \Omega_\text{D}}} \newcommand{\argmin}{\operatorname*{arg\,min}}\)

Download sources
Variational formulation#
There exist different ways of writing a variational formulation in a finite-strain setting depending on the chosen geometric configuration and strain measures. Here, we will use a total Lagrangian formulation and therefore naturally write equilibrium on the reference configuration which we still denote \(\Omega\).
Weak equilibrium reads here:
Find \(\bu \in V\) such that:
\[\begin{equation*} \int_\Omega \bP(\bu):\nabla \bv \dOm = \int_\Omega \boldsymbol{f}\cdot\bv \dOm + \int_\Neumann \bT\cdot\bv \dS \quad \forall \bv \in V_0 \end{equation*}\]
where \(\bP(\bu)\) denotes the first Piola-Kirchhoff (PK1) stress.
Moreover, in the case of a hyperelastic material, the constitutive relation derives from a free-energy potential \(\psi(\bF)\) depending on the deformation gradient \(\bF = \bI + \nabla \bu\). The above non-linear variational equation corresponds in fact to the first-order optimality condition of the following minimum principle:
\[\begin{equation*} \min_{\bu\in V} \int_\Omega \psi(\bF) \dOm - \int_\Omega \boldsymbol{f}\cdot\bu \dOm - \int_\Neumann \bT\cdot\bu \dS \end{equation*}\]
which we will use in the subsequent implementation.
Problem position#
We consider a cylinder of square cross-section which is fixed at its bottom face and to which we impose a rigid rotation of the top face of angle \(\theta\) around the vertical axis. We start first with a simple compressible neo-Hookean model given by:
where \(I_1 = \tr(\bC) = \tr(\bF\T\bF)\) and \(J = \det\bF\).
Implementation#
We load the relevant modules and useful functions and setup the corresponding box mesh. In the following, we will use hexahedra of degree 1.
import numpy as np
import ufl
from mpi4py import MPI
from dolfinx import fem, io, nls
import dolfinx.fem.petsc
import dolfinx.nls.petsc
from dolfinx.mesh import create_box, CellType
from ufl import (
as_matrix,
dot,
cos,
sin,
SpatialCoordinate,
Identity,
grad,
ln,
tr,
det,
variable,
derivative,
TestFunction,
TrialFunction,
)
L = 3.0
N = 4
mesh = create_box(
MPI.COMM_WORLD,
[[-0.5, -0.5, 0.0], [0.5, 0.5, L]],
[N, N, 4 * N],
CellType.hexahedron,
)
dim = mesh.topology.dim
print(f"Mesh topology dimension d={dim}.")
degree = 1
shape = (dim,)
V = fem.functionspace(mesh, ("P", degree, shape))
u = fem.Function(V, name="Displacement")
Mesh topology dimension d=3.
INFO: Disabling color, you really want to install colorlog.
Next, we define the corresponding hyperelastic potential using UFL operators. We can easily obtain the UFL expression for the PK1 stress by differentiating the potential \(\psi\) (1) with respect to the deformation gradient \(\bF\). We therefore declare it as a variable using ufl.variable and then compute \(\bP = \dfrac{\partial \psi}{\partial \bF}\) using ufl.diff.
# Identity tensor
Id = Identity(dim)
# Deformation gradient
F = variable(Id + grad(u))
# Right Cauchy-Green tensor
C = F.T * F
# Invariants of deformation tensors
I1 = tr(C)
J = det(F)
# Shear modulus
E = 1e4
nu = 0.4
mu = fem.Constant(mesh, E / 2 / (1 + nu))
lmbda = fem.Constant(mesh, E * nu / (1 - 2 * nu) / (1 + nu))
# Stored strain energy density (compressible neo-Hookean model)
psi = mu / 2 * (I1 - 3 - 2 * ln(J)) + lmbda / 2 * (J - 1) ** 2
# PK1 stress = d_psi/d_F
P = ufl.diff(psi, F)
print(P)
d/d[var0(I + (grad(Displacement)))] ((-3 + (tr({ A | A_{i_8, i_9} = sum_{i_{10}} (var0(I + (grad(Displacement))))[i_{10}, i_9] * ((var0(I + (grad(Displacement))))^T)[i_8, i_{10}] })) + -1 * 2 * ln(det(var0(I + (grad(Displacement)))))) * c_0 / 2 + c_1 / 2 * (-1 + (det(var0(I + (grad(Displacement)))))) ** 2)
Now, we set up the boundary conditions by first identifying the top and bottom dofs. We use Functions to provide the imposed displacement on both faces. For now, such functions are zero.
def bottom(x):
return np.isclose(x[2], 0.0)
def top(x):
return np.isclose(x[2], L)
bottom_dofs = fem.locate_dofs_geometrical(V, bottom)
top_dofs = fem.locate_dofs_geometrical(V, top)
u_bot = fem.Function(V)
u_top = fem.Function(V)
bcs = [fem.dirichletbc(u_bot, bottom_dofs), fem.dirichletbc(u_top, top_dofs)]
We will later update the value of the u_top function based on a UFL expression corresponding to the imposed rigid body rotation. This expression depends on a scalar value \(\theta\) represented as a Constant object. The use of a fem.Expression results in JIT compilation of the code corresponding to the evaluation of this expression at specific points in the reference elements (here the interpolation points of \(V\) i.e. the hexahedron vertices).
x = SpatialCoordinate(mesh)
theta = fem.Constant(mesh, 0.0)
Rot = as_matrix([[cos(theta), sin(theta), 0], [-sin(theta), cos(theta), 0], [0, 0, 1]])
rotation_displ = dot(Rot, x) - x
rot_expr = fem.Expression(rotation_displ, V.element.interpolation_points())
Now, we define the global non-linear potential energy. Note that since we have non-linear expressions, we specify to the measure dx the desired level of accuracy of the quadrature method. Otherwise, FEniCS may use overly conservative estimates of the required number of quadrature points.
Next, we compute the corresponding non-linear residual using the ufl.derivative function which computes the directional derivative in the direction of the TestFunction v.
We also apply it to the residual itself to compute the corresponding consistent tangent bilinear form, usually called the Jacobian in the context of a Newton method. The latter is computed in the direction of the TrialFunction du.
dx = ufl.Measure("dx", domain=mesh, metadata={"quadrature_degree": 4})
E_pot = psi * dx
v = TestFunction(V)
du = TrialFunction(V)
Residual = derivative(
E_pot, u, v
) # This is equivalent to Residual = inner(P, grad(v))*dx
Jacobian = derivative(Residual, u, du)
Finally, we set up a NonlinearProblem instance based on the corresponding residual and jacobian, unknown function and boundary conditions. The latter will also be attached to a nonlinear solver implementing a Newton method.
problem = fem.petsc.NonlinearProblem(Residual, u, bcs)
solver = nls.petsc.NewtonSolver(mesh.comm, problem)
# Set Newton solver options
solver.atol = 1e-4
solver.rtol = 1e-4
solver.convergence_criterion = "incremental"
We are now in position to write the load-stepping loop which simply updates the value of \(\theta\). Since, rot_expr is symbolically linked to theta, this new value is automatically accounted for when interpolating the imposed top displacement from rot_expr.
angle_max = 2 * np.pi
Nsteps = 15
out_file = "hyperelasticity.xdmf"
with io.XDMFFile(mesh.comm, out_file, "w") as xdmf:
xdmf.write_mesh(mesh)
u.vector.set(0.0)
for n, angle in enumerate(np.linspace(0, angle_max, Nsteps + 1)[1:]):
theta.value = angle
u_top.interpolate(rot_expr)
num_its, converged = solver.solve(u)
assert converged
u.x.scatter_forward() # updates ghost values for parallel computations
print(
f"Time step {n}, Number of iterations {num_its}, Angle {angle*180/np.pi:.0f} deg."
)
with io.XDMFFile(mesh.comm, out_file, "a") as xdmf:
xdmf.write_function(u, n + 1)
Time step 0, Number of iterations 5, Angle 24 deg.
Time step 1, Number of iterations 5, Angle 48 deg.
Time step 2, Number of iterations 5, Angle 72 deg.
Time step 3, Number of iterations 5, Angle 96 deg.
Time step 4, Number of iterations 5, Angle 120 deg.
Time step 5, Number of iterations 5, Angle 144 deg.
Time step 6, Number of iterations 5, Angle 168 deg.
Time step 7, Number of iterations 6, Angle 192 deg.
Time step 8, Number of iterations 6, Angle 216 deg.
Time step 9, Number of iterations 6, Angle 240 deg.
Time step 10, Number of iterations 6, Angle 264 deg.
Time step 11, Number of iterations 6, Angle 288 deg.
Time step 12, Number of iterations 6, Angle 312 deg.
Time step 13, Number of iterations 6, Angle 336 deg.
Time step 14, Number of iterations 6, Angle 360 deg.
Exercise#
Change the hyperelasticity model to another version of a compressible neo-Hookean model:
where \(\overline{I}_1 = \tr(\overline{\bC})\) with \(\overline{\bC} = J^{-2/3}\bC\).