Create a piecewise constant field for spatially varying properties#
Objectives
We provide here a utility function to create a piecewise constant field for each region of a domain
Download sources
import numpy as np
import matplotlib.pyplot as plt
from mpi4py import MPI
from dolfinx import mesh, fem
def create_piecewise_constant_field(domain, cell_markers, property_dict, name=None):
"""Create a piecewise constant field with different values per subdomain.
Parameters
----------
domain : Mesh
`dolfinx` mesh object
cell_markers : MeshTag
cell marker MeshTag
property_dict : dict
A dictionary mapping region tags to physical values {tag: value}
Returns
-------
A DG-0 function
"""
V0 = fem.functionspace(domain, ("DG", 0))
k = fem.Function(V0, name=name)
for tag, value in property_dict.items():
cells = cell_markers.find(tag)
k.x.array[cells] = np.full_like(cells, value, dtype=np.float64)
return k
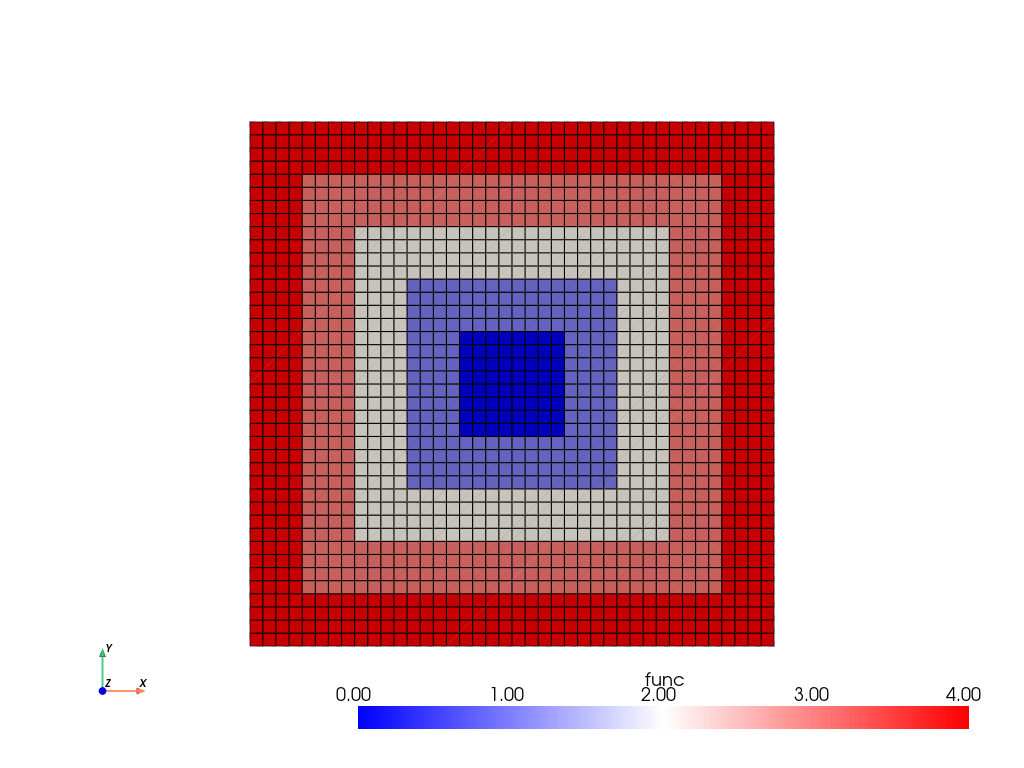
For instance, we first create a square mesh and define a geometric marker marking a square strip of inner radius a and outer radius b:
N = 40
domain = mesh.create_unit_square(
MPI.COMM_WORLD, N, N, cell_type=mesh.CellType.quadrilateral
)
def strip(x, a, b, eps=1e-8):
return np.logical_and(
np.logical_and(np.abs(x[0] - 0.5) <= b + eps, np.abs(x[1] - 0.5) <= b + eps),
np.logical_or(np.abs(x[0] - 0.5) >= a - eps, np.abs(x[1] - 0.5) >= a - eps),
)
We then use the function mark_entities introduced in Marking facets with geometrical functions to mark the corresponding cells and create a piecewise constant field.
Show code cell source
def mark_entities(domain, dim, entities_dict):
"""Mark entities of specified dimension according to geometrical location
Parameters
----------
domain : Mesh
`dolfinx` mesh object
dim : int
Dimension of the entities to mark
entities_dict : dict
A dictionary mapping integer tags with geometrical location function {tag: locator(x)}
Returns
-------
entities_tag array
"""
marked_values = []
marked_entities = []
# number of non-ghosted entities
num_entities_local = domain.topology.index_map(dim).size_local
# Concatenate and sort the arrays based on indices
for tag, location in entities_dict.items():
entities = mesh.locate_entities(domain, dim, location)
entities = entities[entities < num_entities_local] # remove ghost entities
marked_entities.append(entities)
marked_values.append(np.full_like(entities, tag))
marked_entities = np.hstack(marked_entities)
marked_values = np.hstack(marked_values)
sorted_entities = np.argsort(marked_entities)
entities_tags = mesh.meshtags(
domain, dim, marked_entities[sorted_entities], marked_values[sorted_entities]
)
return entities_tags
tdim = domain.topology.dim
cell_markers = mark_entities(
domain,
tdim,
{
0: lambda x: strip(x, 0, 0.1),
1: lambda x: strip(x, 0.1, 0.2),
2: lambda x: strip(x, 0.2, 0.3),
3: lambda x: strip(x, 0.3, 0.4),
4: lambda x: strip(x, 0.4, 0.5),
},
)
func = create_piecewise_constant_field(
domain, cell_markers, {k: float(k) for k in range(5)}
)
Show code cell source
import pyvista
from dolfinx import plot
pyvista.set_jupyter_backend("static")
topology, cell_types, geometry = plot.vtk_mesh(domain, 2)
grid = pyvista.UnstructuredGrid(topology, cell_types, geometry)
grid.cell_data["func"] = func.x.array
grid.set_active_scalars("func")
# Create plotter and pyvista grid
p = pyvista.Plotter()
p.add_mesh(grid, show_edges=True, cmap="bwr")
p.view_xy()
p.show_axes()
p.show()