Thermo-elastic evolution problem (full coupling)

Thermo-elastic evolution problem (full coupling) #

Objectives

This demo shows how to solve a transient thermoelastic evolution problem in which both thermo-mechanical fields are fully coupled. \(\newcommand{\bsig}{\boldsymbol{\sigma}} \newcommand{\beps}{\boldsymbol{\varepsilon}} \newcommand{\bu}{\boldsymbol{u}} \newcommand{\bv}{\boldsymbol{v}} \newcommand{\bT}{\boldsymbol{T}} \newcommand{\bI}{\boldsymbol{I}} \newcommand{\T}{^\text{T}} \newcommand{\tr}{\operatorname{tr}} \newcommand{\CC}{\mathbb{C}} \newcommand{\dOm}{\,\text{d}\Omega} \newcommand{\dS}{\,\text{d}S} \newcommand{\Neumann}{{\partial \Omega_\text{N}}} \newcommand{\Dirichlet}{{\partial \Omega_\text{D}}}\)

Download sources

Introduction#

We will assume that the evolution is quasi-static and will hence neglect inertial effects. Note that a staggered approach could also have been adopted in which one field is calculated first (say the temperature for instance) using predicted values of the other field and similarly for the other field in a second step (see for instance [Farhat et al., 1991]).

Problem position#

The problem consists of a quarter of a square plate perforated by a circular hole. Thermo-elastic properties are isotropic and correspond to those of aluminium (note that stress units are in \(\text{MPa}\), distances in \(\text{m}\) and mass in \(\text{kg}\)). Linearized thermo-elasticity will be considered around a reference temperature of \(T_0 = 293 \text{ K}\). A temperature increase of \(\Delta T=+10^{\circ}\text{C}\) will be applied on the hole boundary. Symmetry conditions are applied on the corresponding symmetry planes and stress and flux-free boundary conditions are adopted on the plate outer boundary.

We first import the relevant modules.

import matplotlib.pyplot as plt
import numpy as np
import gmsh
from mpi4py import MPI
import basix
import ufl
from dolfinx import fem, mesh, io, nls
from dolfinx.io.gmshio import model_to_mesh

import dolfinx.fem.petsc
import dolfinx.nls.petsc

The mesh is then defined using the gmsh Python API.

We now define the relevant function space for the considered problem. Since we will adopt a monolithic approach i.e. in which both fields are coupled and solved at the same time, we will need to resort to a mixed function space for both the displacement \(\boldsymbol{u}\) and the temperature variation \(\Theta=T-T_0\).

Variational formulation and time discretization#

The linearized thermoelastic constitutive equations are given by:

\[ \boldsymbol{\sigma} = \mathbb{C}:(\boldsymbol{\varepsilon}-\alpha(T-T_0)\boldsymbol{1}) = \lambda\text{tr}(\boldsymbol{\varepsilon})\boldsymbol{1}+2\mu\boldsymbol{\varepsilon} -\kappa(T-T_0)\boldsymbol{1} \]

\[ \rho s = \rho s_0 + \dfrac{\rho C_{\varepsilon}}{T_0}(T-T_0) + \kappa\text{tr}(\boldsymbol{\varepsilon}) \]

\(\lambda,\mu\) the Lamé coefficients
\(\rho\) material density
\(\alpha\) thermal expansion coefficient
\(\kappa = \alpha(3\lambda+2\mu)\)
\(C_{\varepsilon}\) the specific heat at constant strain (per unit of mass).
\(s\) (resp. \(s_0\)) the entropy per unit of mass in the current (resp. initial configuration)

These equations are completed by the equilibrium equation which will later be expressed in its weak form (virtual work principle) and the linearized heat equation (without source terms):

\[ \rho T_0 \dot{s} + \text{div} \boldsymbol{q}= 0 \]

where the heat flux is related to the temperature gradient through the isotropic Fourier law: \(\boldsymbol{q} = - k\nabla T\) with \(k\) being the thermal conductivity. Using the entropy constitutive relation, the weak form of the heat equation reads as:

\[ \int_{\Omega}\rho T_0 \dot{s}\widehat{T}d\Omega - \int_{\Omega} \boldsymbol{q}\cdot\nabla \widehat{T}d\Omega= -\int_{\partial \Omega} \boldsymbol{q}\cdot\boldsymbol{n} \widehat{T} dS \quad \forall \widehat{T} \in V_T \]

\[ \int_{\Omega}\left(\rho C_{\varepsilon}\dot{T} + \kappa T_0\text{tr}(\dot{\boldsymbol{\varepsilon}})\right) \widehat{T}d\Omega + \int_{\Omega} k \nabla T\cdot\nabla \widehat{T}d\Omega= \int_{\partial \Omega} k\partial_n T \widehat{T} dS \quad \forall \widehat{T} \in V_T \]

with \(V_T\) being the FunctionSpace for the temperature field.

The time derivatives are now replaced by an implicit Euler scheme, so that the previous weak form at the time increment \(n+1\) is now:

(9)#\[\int_{\Omega}\left(\rho C_{\varepsilon}\dfrac{T-T_n}{\Delta t} + \kappa T_0\text{tr}\left(\dfrac{\boldsymbol{\varepsilon}-\boldsymbol{\varepsilon}_n}{\Delta t}\right)\right) \widehat{T}d\Omega + \int_{\Omega} k \nabla T\cdot\nabla \widehat{T}d\Omega= \int_{\partial \Omega} k\partial_n T \widehat{T} dS \quad \forall \widehat{T} \in V_T\]

where \(T\) and \(\boldsymbol{\varepsilon}\) correspond to the unknown fields at the time increment \(n+1\). For more details on the time discretization of the heat equation, see also the Heat equation FEniCS tutorial.

In addition to the previous thermal weak form, the mechanical weak form reads as:

(10)#\[\int_{\Omega} \left(\lambda\text{tr}(\boldsymbol{\varepsilon})\boldsymbol{1}+2\mu\boldsymbol{\varepsilon} -\kappa(T-T_0)\boldsymbol{1}\right) :\nabla^s\widehat{\boldsymbol{v}}\text{ d} \Omega = W_{ext}(\widehat{\boldsymbol{v}}) \quad \forall \widehat{\boldsymbol{v}}\in V_U\]

where \(V_U\) is the displacement FunctionSpace and \(W_{ext}\) the linear functional corresponding to the work of external forces.

The solution of the coupled problem at \(t=t_{n+1}\) is now \((\boldsymbol{u}_{n+1},T_{n+1})=(\boldsymbol{u},T)\in V_U\times V_T\) verifying (9) and (10). These two forms are implemented below with zero right-hand sides (zero Neumann BCs for both problems here). One slight modification is that the temperature unknown \(T\) is replaced by the temperature variation \(\Theta=T-T_0\) which appears naturally in the stress constitutive relation. Note that we use here a NonlinearProblem to be more general.

v = fem.Function(V)
(u, Theta) = ufl.split(v)
v_ = ufl.TestFunction(V)
(u_, Theta_) = ufl.split(v_)
dv = ufl.TrialFunction(V)

V_aux = fem.functionspace(domain, ("DG", 1))
s_old = fem.Function(V_aux, name="Previous_entropy")


def eps(u):
    return ufl.sym(ufl.grad(u))


E = fem.Constant(domain, 70e3)
nu = fem.Constant(domain, 0.3)
k = fem.Constant(domain, 237e-6)
rho = fem.Constant(domain, 2700.0)
alpha = fem.Constant(domain, 2.31e-5)
cV = fem.Constant(domain, 910e-6)

lmbda = E * nu / (1 + nu) / (1 - 2 * nu)
mu = E / 2 / (1 + nu)
kappa = alpha * (3 * lmbda + 2 * mu)

sig = (
    lmbda * ufl.tr(eps(u)) * ufl.Identity(gdim)
    + mu * eps(u)
    - kappa * Theta * ufl.Identity(gdim)
)
j = -k * ufl.grad(Theta)

s = cV / Tref * Theta + kappa / rho * ufl.tr(eps(u))
s_expr = fem.Expression(s, V_aux.element.interpolation_points())

mech_res = ufl.inner(sig, eps(u_)) * ufl.dx
therm_res = (
    rho * Tref_value * (s - s_old) / dt * Theta_ - ufl.dot(j, ufl.grad(Theta_))
) * ufl.dx
Res = mech_res + therm_res
Jac = ufl.derivative(Res, v, dv)


problem = fem.petsc.NonlinearProblem(Res, v, bcs=bcs, J=Jac)

newton = nls.petsc.NewtonSolver(domain.comm, problem)
newton.rtol = 1e-8
newton.atol = 1e-8
newton.convergence_criterion = "incremental"
newton.report = True
newton.max_it = 10
ksp = newton.krylov_solver

Resolution#

The problem is now solved by looping over time increments. Because of the typical exponential time variation of temperature evolution of the heat equation, time steps are discretized on a non-uniform (logarithmic) scale. \(\Delta t\) is therefore updated at each time step. Note that since we work in terms of temperature variation and not absolute temperature all fields can be initialized to zero, otherwise \(T\) would have needed to be initialized to the reference temperature \(T_0\).

Nincr = 50
t = np.logspace(1, 4, Nincr + 1)
x = V_t.tabulate_dof_coordinates()[bottom_T_dofs, 0]  # x position of dofs
T_res = np.zeros((len(x), Nincr + 1))

vtk_d = io.VTKFile(domain.comm, "displacement.pvd", "w")
vtk_T = io.VTKFile(domain.comm, "temperature.pvd", "w")

for i, dti in enumerate(np.diff(t)):
    dt.value = dti

    num_its, converged = newton.solve(v)
    assert converged

    s_old.interpolate(s_expr)

    u_out = v.sub(0).collapse()
    u_out.name = "Displacement"
    T_out = v.sub(1).collapse()
    T_out.name = "Temperature variation"

    # vtk_d.write_function(u_out, i)
    # vtk_T.write_function(T_out, i)

    T_res[:, i + 1] = T_out.vector.array[bottom_T_dofs]

vtk_d.close()
vtk_T.close()

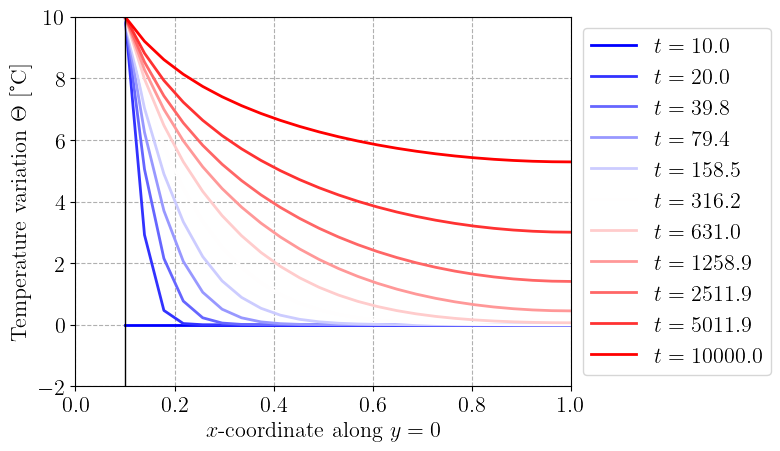
At each time increment, the variation of the temperature increase \(\Theta\) along a line \((x, y=0)\) is saved in the T_res array. This evolution is plotted below. As expected, the temperature gradually increases over time, reaching eventually a uniform value of \(+10^{\circ}\text{C}\) over infinitely long waiting time.

t_plot = t[:: Nincr // 10]
plt.gca().set_prop_cycle(color=plt.cm.bwr(np.linspace(0, 1, len(t_plot))))
plt.plot(x, T_res[:, :: Nincr // 10], label=[rf"$t={ti:.1f}$" for ti in t_plot])
plt.axvline(x=0.1, color="k", linewidth=1)
plt.legend(bbox_to_anchor=(1.0, 1.0))
plt.xlabel(r"$x$-coordinate along $y=0$")
plt.ylabel(r"Temperature variation $\Theta$ [°C]")
plt.show()

../../../_images/a85dfb3a88c1a02a138c297ac29462b9b8f0099409764324f34699c55e22dad6.png

References#

[FPDP91]

Charbel Farhat, KC Park, and Yves Dubois-Pelerin. An unconditionally stable staggered algorithm for transient finite element analysis of coupled thermoelastic problems. Computer methods in applied mechanics and engineering, 85(3):349–365, 1991. doi:10.1016/0045-7825(91)90102-C.